找课后习题答案,就上大学教材课后答案网!
查看完整版: 高等数学第六版课后习题答案
高等数学第六版课后习题答案
 第1章 函数与极限
第1章 函数与极限
 1.1 复习笔记
1.1 复习笔记
一、映射与函数
1.集合
(1)集合概念
集合(简称集)是指具有某种特定性质的事物的总体,组成这个集合的事物称为该集合的元素(简称元)。常用大写拉丁字母A,B,C,…表示集合,用小写拉丁字母a,b,c,…表示集合的元素。
如果a是集合A的元素,就说a属于A,记作a∈A;如果a不是集合A的元素,就说a不属于A,记作a A。
A。
一个集合,若它只含有有限个元素,则称为有限集;不是有限集的集合称为无限集。
(2)表示集合的方法通常有以下两种:
①列举法,就是把集合的全体元素一一列举出来表示;
②描述法,若集合M是由具有某种性质P的元素x的全体所组成的,就可表示成M={x|具有性质P}。
(3)常见的集合
①空集,指不包含任何元素的集合,记为φ;
②非负整数集,全体非负整数即自然数的集合,记作N,即N={0,1,2,…,n,…};
③正整数集,全体正整数的集合,记作 ,即
,即 ={1,2,3,…,n,…};
={1,2,3,…,n,…};
④整数集,全体整数的集合,记作Z,即Z={…,-n,…,-2,-1,0,1,2,…,n,…};
⑤有理数集,全体有理数的集合,记作Q,即Q={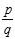 ∈z,q∈
∈z,q∈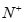 且P与q互质};
且P与q互质};
⑥实数集,全体实数的集合,记作R,R为排除数0的实数集, 为全体正实数的集合。
为全体正实数的集合。
(4)集合的关系
①包含关系
设A、B是两个集合,如果集合A的元素都是集合B的元素,则称A是B的子集,记作A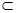 B(读作A包含于B)或B
B(读作A包含于B)或B A(读作B包含A)。规定空集φ是任何集合A的子集,即φ
A(读作B包含A)。规定空集φ是任何集合A的子集,即φ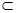 A。
A。
若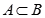 且
且 ,则称A是B的真子集,记作
,则称A是B的真子集,记作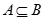 (读作A真包含于B)。
(读作A真包含于B)。
②等价关系
若集合A与集合B互为子集,即A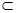 B且B
B且B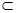 A,则称集合A与集合B相等,记作A=B。
A,则称集合A与集合B相等,记作A=B。
(5)集合的运算
①并、交、差
a.并集
设A、B是两个集合,由所有属于A或者属于B的元素组成的集合,称为A与B的并集(简称并),记作 ,即
,即 。
。
b.交集
由所有既属于A又属于B的元素组成的集合,称为A与B的交集(简称交),记作 ,即
,即

。
c.差集
由所有属于A而不属于B的元素组成的集合,称为A与B的差集(简称差),记作A\B,即
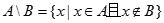 。若集合I为全集或基本集,称I\A为A的余集或补集,记作AC。
。若集合I为全集或基本集,称I\A为A的余集或补集,记作AC。
②集合的运算法则
设A、B、C为任意三个集合,则有下列法则成立:

③笛卡尔积
设A、B是任意两个集合,在集合A中任意取一个元素x,在集合B中任意取一个元素y,组成一个有序对(x,y),把这样的有序对作为新的元素,它们全体组成的集合称为集合A与集合B的笛卡尔积,记为A×B,即
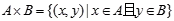
。
(6)区间和邻域
①区间
a.开区间
设a和b都是实数,且a<b,数集{x|a<x<b}称为开区间,记作(a,b),即(a,b)={x|a<x<b}。其中a和b称为开区间(a,b)的端点,这里 ,
,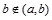 。
。
b.闭区间
数集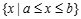 称为闭区间,记作[a,b],即
称为闭区间,记作[a,b],即 。其中a和b称为闭区间[a,b]的端点,这里a∈[a,b],b∈[a,b]。
。其中a和b称为闭区间[a,b]的端点,这里a∈[a,b],b∈[a,b]。
c.半开区间
定义 ,
,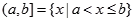 ,[a,b)和(a,b]都称为半开区间。前者也称为前闭后开区间,后者也称为前开后闭区间。
,[a,b)和(a,b]都称为半开区间。前者也称为前闭后开区间,后者也称为前开后闭区间。
d.区间长度
对于有限区间(a,b),数b-a称为区间长度。对于无限区间,引进记号十∞(读作正无穷大)及-∞(读作负无穷大),其区间长度为∞。全体实数的集合R也可记作(-∞,+∞),它也是无限区间。
查看完整版: 高等数学第六版课后习题答案
高等数学第六版课后习题答案
相关资料推荐
- 同济大学数学系《高等数学》(第7版)(上册)精讲班【教材精讲+考研真题串讲】
- 同济大学数学系《高等数学》(第7版)笔记和课后习题(含考研真题)详解
- 同济大学数学系《高等数学》(第6版)(上册)笔记和课后习题(含考研真题)详解
- 同济大学数学系《高等数学》(第6版)(下册)笔记和课后习题(含考研真题)详解
- 贾俊平统计学第七版课后答案解析-大学教材课后答案网2021-07-11


