高等数学同济大学第七版习题答案_复习笔记pdf

五、极限运算法则

1极限运算法则相关定理

（1）定理1

两个无穷小的和是无穷小，有限个无穷小之和也是无穷小。

（2）定理2

有界函数与无穷小的乘积是无穷小。

①推论1：常数与无穷小的乘积是无穷小。

②推论2：有限个无穷小的乘积是无穷小。

（3）定理3

如果limf（x）＝A，limg（x）＝B，则

①lim[f（x）±g（x）]＝limf（x）±limg（x）＝A±B；

②lim[f（x）·g（x）]＝limf（x）·limg（x）＝A·B；

③若又有B≠0，则lim（f（x）/g（x））＝limf（x）/limg（x）＝A/B

a．推论1：如果limf（x）存在，而c为常数，则lim[cf（x）]＝climf（x）；

b．推论2：如果存在，而n是正整数，则lim[f（x）]ⁿ＝[limf（x）]ⁿ。

六、极限存在准则及两个重要极限

1极限存在准则

（1）夹逼准则

①夹逼准则1

如果数列{x_n}，{y_n}及{z_n}满足下列条件：

a．从某项起，即∃n₀∈N_＋，当n＞n₀时，有y_n≤x_n≤z_n；

b．，则数列{x_n}的极限存在，且。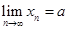

②夹逼准则2

a．当x∈U°（x₀，r）（或|x|＞M）时，g（x）≤f（x）≤h（x）；

b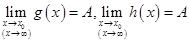．，则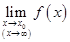存在，且等于A。

（2）单调有界准则

单调有界数列必有极限。

（3）左极限存在准则

设函数f（x）在点x₀的某个左邻域内单调并且有界，则f（x）在x₀的左极限f（x₀^－）必定存在。

（4）柯西极限存在准则

数列{x_n}收敛的充分必要条件是：对于任意给定的正数ε，存在正整数N，使得当m＞N，n＞N时，有|x_n－x_m|＜ε。

（7）幂指函数的极限

一般地，对于形如u（x）^v（x）（u（x）＞0，u（x）≠1）的函数（通常称为幂指函数），如果limu（x）＝a＞0，limv（x）＝b，limu（x）^v（x）＝a^b。

注：这里三个lim都表示在同一自变量变化过程中的极限。

4有关sinx，x，tanx的不等式

sinx＜x＜tanx，∀x∈（－π/2，0）或（0，π/2）

十、闭区间上连续函数的性质

1函数f（x）在闭区间[a，b]上连续

如果函数f（x）在开区间（a，b）内连续，在右端点b左连续，在左端点a右连续，则函数f（x）就是在闭区间[a，b]上连续。

2闭区间上连续函数的性质（见表1-4）

表1-4 闭区间上连续函数的性质

3一致连续性

（1）一致连续与连续的关系

如果函数f（x）在区间I上一致连续，则f（x）在区间I上一定连续；当f（x）在区间I上连续，f（x）在区间I上不一定一致连续。

（2）一致连续性定理

如果函数f（x）在闭区间[a，b]上连续，则它在该区间上一致连续。

第1章 函数与极限

 1.1 复习笔记

 1.2 课后习题详解

 1.3 考研真题详解

第2章 导数与微分

 2.1 复习笔记

 2.2 课后习题详解

 2.3 考研真题详解

第3章 微分中值定理与导数的应用

 3.1 复习笔记

 3.2 课后习题详解

 3.3 考研真题详解

第4章 不定积分

 4.1 复习笔记

 4.2 课后习题详解

 4.3 考研真题详解

第5章 定积分

 5.1 复习笔记

 5.2 课后习题详解

 5.3 考研真题详解

第6章 定积分的应用

 6.1 复习笔记

 6.2 课后习题详解

 6.3 考研真题详解

第7章 微分方程

 7.1 复习笔记

 7.2 课后习题详解

 7.3 考研真题详解

第8章 向量代数与空间解析几何

 8.1 复习笔记

 8.2 课后习题详解

 8.3 考研真题详解

第9章 多元函数微分法及其应用

 9.1 复习笔记

 9.2 课后习题详解

 9.3 考研真题详解

第10章 重积分

 10.1 复习笔记

 10.2 课后习题详解

 10.3 考研真题详解

第11章 曲线积分与曲面积分

 11.1 复习笔记

 11.2 课后习题详解

 11.3 考研真题详解

第12章 无穷级数

 12.1 复习笔记

 12.2 课后习题详解

 12.3 考研真题详解